Fibonacci retracement

Fibonacci numbers are the legendary sequence 0, 1, 1, 2, 3, 5, 8, 11, ... , named after Leonardo of Pisa, also known as Fibonacci, filius Bonacci, "son of Bonaccio". The sequence is given by the recursive formula:

with starting values:

As you can imagine Fibonacci numbers have also application in economics. Here is what wikipedia* says:

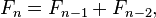
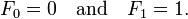
"In financial mathematics, Fibonacci retracements are a method of technical analysis. They are named after their use of the Fibonacci sequence. Fibonacci retracement levels are based on Fibonacci ratios.

Fibonacci retracement is based on the idea that markets will retrace a predictable portion of a move, after which they will continue to move in the original direction.

These pullbacks are often traded or used as an opportunity to position for the direction of the original move.

Fibonacci retracements occur at distinct levels of the original move. Each Fibonacci level is considered to be an area where the market will likely find levels of support or resistance.

The four basic Fibonacci retracement levels are calculated as 23.6%, 38.2% 50.0% and 61.8%, signifying the portion of the move in the opposite direction of the original move. 0.0% is considered to be the start of the retracement, while 100.0% is a complete reversal to the original part of the move."

But what about the tribonacci numbers? These are similar to the Fibonacci numbers but including three terms in the sum. Do they have an application in finance? And what about the generalization of this sequence?

* This content is available under the Creative Commons Attribution-ShareAlike License.